What makes Automated Planning complex?

24 Jul 2022

Automated planning is a branch of artificial intelligence that concerns the generation of action sequences, typically for execution by intelligent agents, autonomous robots and unmanned vehicles, which allows the achievement of a set of objectives called goals. Unlike classical control and classification problems, plannins is usually a really complex task. What is that makes this task so complex?

In 1973, in his PhD thesis, Gerald Jay Sussman shows some problems of the planners of the time, subsequently defined, in his honor, Sussman anomaly [1].

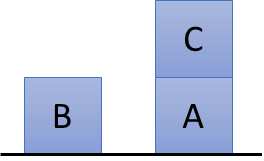
In order to describe these issues, suppose we are in a blocks world, a world, typically used in automated planning, in which there are some blocks on a table and the goal is to build one or more vertical stacks of blocks. Possible world states can be described by a set of literals considered true in a particular state, assuming, in a typical closed-world assumption, that literals not explicitly declared as true are false. The initial state, in particular, graphically shown in the following image, could be described by means of the $OnTable\left(A\right)$, the $OnTable\left(B\right)$ and the $On\left(A, C\right)$ literals.

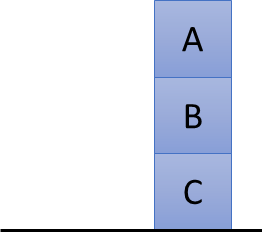
The agent can take the blocks, move them on the table or stack them on other blocks. The assumption, however, is that blocks have weight and, therefore, you can only take blocks that have no other blocks above them. Suppose now we want to generate a sequence of actions (i.e., a plan) whose execution would achieve the objective, graphically shown in the following image, described by the $On\left(C, B\right)$ and the $On\left(B, A\right)$ literals.

The agent may think of achieving the two goals independently, achieving, initially, the first goal and, then, the other. Suppose, for example, that the $On\left(C, B\right)$ goal is chosen as first. To this end, the agent takes $B$ block, initially on the table, and stacks it on block $C$, easily achieving, as graphically shown in the following image, the $On\left(C, B\right)$ goal.

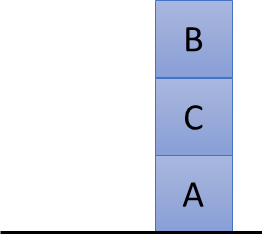
Once block $B$ is stacked on top of block $C$, however, block $A$ gets stuck under the weight of blocks $B$ and $C$. Not being able to move block $A$, clearly, the $On\left(B, A\right)$ goal remains unachievable.

A similar problem could have occurred even if, instead of the $On\left(C, B\right)$ goal, the $On\left(B, A\right)$ goal would have been chosen as first. Block $C$, in particular, could be picked up and moved on the table.

Block $A$ could then be picked up and stacked on block $B$.

In this case block $B$ gets stuck under the weight of block $A$, making the $On\left(C, B\right)$ goal remains unachievable.

The solution to this problem, therefore, is to consider the different goals at the same time, taking into account the interactions they may have among them. Managing all the goals together, however, makes solving a planning problem hard from a computational complexity point of view (depending on the expressiveness managed by the solvers, from PSPACE-complete on [2]).

A broader view

The Sussman anomaly, to date, is handled by any modern planner. It remains, nonetheless, still useful for explaining why planning is non-trivial. To better understand such complexity it might be useful to see the Sussman anomaly as a particular case of a broader problematic. Understanding these issues allows us to study better heuristics to solve planning problems more efficiently and, more generally, to understand how some phenomena work in the world around us. The broader problem, indeed, is applicable in all those situations in which you have to move away from the solution to get closer to it.

Imagine, for example, the following sadistic situation. There is a dog and, beyond a gate, a nice succulent bone.

The gate is, on one side, far from the bone, open. In order to reach the bone, hence, the dog should first move away from the bone and, once through the gate, get closer and easily reach the tasty booty. However, the dog sees the bone through the gate and smells it. The closer it gets to the bone, the more difficult it will be to move away from it. Whenever the poor dog moves away from the bone to look for an alternative to reach the meal it will see the bone go away, the bone’s smell will be fading and, therefore, the dog will end up believing that it is moving in the wrong direction, getting back “closer” to the bone.

In a scenario like this, Sussman’s anomaly is represented by the gate that forces the dog, if it wants to reach the bone, to temporarily move away from the desired target. The same problem, nonetheless, occurs also in the case of optimization in all those situations (the overwhelming majority) in which, in the optimization function, local minima occur. Suppose we are trekking on a mountain when, suddenly, the fog descends, preventing us from seeing beyond a few meters. We don’t have a compass and our GPS battery has run out. Additionally, we do not know the area very well, yet we know that our vehicle is downstream and, to return safely to our homes, we must reach it.

If we are particularly lucky, the mountain could have a shape like the one depicted in the following picture. Although with a profile that is not perfectly regular like the one in the figure, the mountain could still have a path similar to that of a convex function.

In this case, of course, wherever we were, we would have to do nothing but go down! It is difficult to demonstrate intelligent behavior in these cases, as even a fairly round stone would be able to return home. It should only roll, taking advantage of gravity, while letting itself be guided by the slope of the mountain.

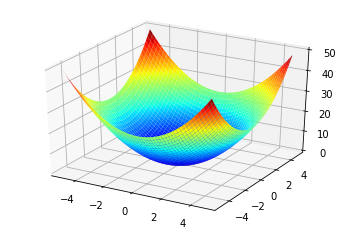
The situation would become risky, although more interesting, if we were on a mountain with a profile similar to that of the following figure. This shape is typically called the Ackley function and is often used to test the capabilities of the optimization algorithms.

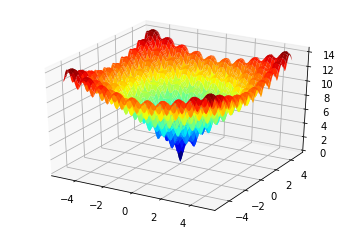
In this case, in particular, we wouldn’t know where to go! We could not superficially exploit the information coming from the slope of the mountain because, almost certainly, we would end up in a local minimum. Any attempt to reach our vehicle, moreover, would almost certainly require the need to take some steps uphill, forcing us to move away from the lowest point to, hopefully, getting closer to it, later, and, eventually, finally reach the destination.

Conclusions

Planning a sequence of actions to achieve a certain set of goals is a potentially demanding task from a combinatorial point of view. The complexity derives from the expressiveness of the language chosen to define the planning problem and, more in detail, from the possibility of expressing the potential interactions that any objectives may have.

The development of domain-independent heuristics allows to alleviate the negative effects generated by this complexity but, in order to be correctly evaluated, it is necessary to apply them to evaluation problems capable of challenging the abilities of planners, equipped with “gates” that prevent poor dogs from directly reach the desired bones and local minima that make any hikers run the risk of getting lost. As smart as your approach may be, evaluating it on an extremely simple problem, like in the case of a convex function, you may not realize that, actually, on more complex cases, your algorithm does not work well as you expected.

References

[1] Sussman, G. J. (1973). A computational model of skill acquisition (pdf).

[2] Bylander, T. (1994). The computational complexity of propositional STRIPS planning. Artificial Intelligence. 69 (1-2). 165-204 https://doi.org/10.1016/0004-3702(94)90081-7.